And so unsurprisingly it has a special place in the hearts of many mathematicians. The 16th century German mathematician Ludoph van Ceulen even had his tombstone engraved with his 32 decimal place estimations of pi.
Ah, Pi!
Fiercely irrational, blissfully transcendent, and so essential to the universe and how it works...
But it's so tricky. Oh course, I know how to write Pi's true form, but instead of revealing that truth to you and thus blowing your minds, I'll just share with you some other def.s of pi, beyond just the ratio of the perimeter of a circle and its diameter (meter! meter!) (all better than the old stand-by 3.14).
1. Good old Archimedes came up with a rough estimate: π is between 223/71 and 22/7
He figured this by drawing a circle, drawing a polygram inside the circle, touching all the sides, and then drawing a polygram outside the circle where the circle touched all of its sides. Then he compared the two polygrams, and by making more and more sides... and this is how you get the rough estimate 22/7 which I used through much of elementary school.
2. Here's one an Indian did write up in the 15th century AD:
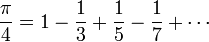 and so on... FOREVER!!!
and so on... FOREVER!!!Pretty damn awesome. INFINITE SERIES RULE!!!
Good work Madhava of Sangamagrama! It would take until the 17th century for the series to be rediscovered through the hearty work of James Gregory and Gottfried Leibniz.
3. And if you like your arctangents (and who doesn't?), how about this def. of pi:
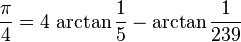
Kudos John Machin!
And if you don't like your arctans, well,
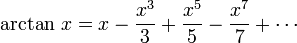 and so on, still FOREVER!!!
and so on, still FOREVER!!! At least according to a nice little Taylor expansion of arctangent.
4. Well, to take Pi to the next level, another Indian had to get into the game. And so in the early 19th century another Indian did (actually Indians had been working all along, but this 5 def.s not a total history). I'm talking about the one, the only Srinivāsa Rāmānujan!!!
Check out his method for finding Pi, derived from the highest halls of Number Theory:
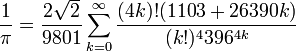
While that method didn't hit the big time till 1985, in that year William Gosper used it to calculate Pi to 17 million digits. Dude, sweet.
5. But if you want to go a little ways by the abstract route. Well, remember that Euler with some Taylor formulization of e^(ix), sin x and cos x, came up with

which when x = pi leads to a nice little identity involving pi:
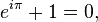
Ah, Euler, you may have lived in the 18th century and pronounced your name like a greaser, but you're still one of the best.
So in conclusion let me give you one more def. of pi:
Pi = Awesome
Exactly
No comments:
Post a Comment